QCC lecture1

量子通讯与密码

Lecture 1

• Bra-ket notation

• Ket - column vector, bra - row vector

• \(<\psi|=|\psi>^{+}\)

• Hilbert space

1. \(<\psi|\psi> >0\) for all \(|\psi>\ne 0\)
2. \(<\phi|(a|\psi_1>+b|\psi_2>)=a<\phi|\psi_1>+b<\phi|\psi_2>\)
3. \(<\phi|\psi>=<\psi|\phi>^*\)

• Ray

• If \(<\psi|\psi>=1\), then \(|\psi>\) is called a ray
• In quantum mechanics, if \(a\ne 0\), then \(a|\psi>, |\psi>\) represent the same state(the overall phase doesn't matter)

• However, note that \(e^{i\theta}|\psi>+|\phi>\ne|\psi>+|\phi>\), where \(e^{i\theta}\) is the relative phase

• State(\(|\psi>\))

• A complete description of a system

• Spin-\(\frac 12\)

• \(|0>\)-up, \(|1>\)-down

• spin-1: H-\(|0>\), V-\(|1>\) (relation between spin-1 & spin-\(\frac 12\))

• Born's rule

• \(|\psi>=a|0>+b|1>\), then the possibility to get
  • \(|0>:\frac{a^2}{a^2+b^2}\)
  • \(|1>:\frac{b^2}{a^2+b^2}\)

• Qudit

• \(|\psi>=\sum_0^{d-1}c_i|i>\)
• Number of real variable parameters: \(2d-2\)
  • Global phase
  • Normalization

• Density matrix

• \(\rho\equiv|\phi><\phi|\), is a \(d\times d\) matrix(where \(|\phi>\) is required to be normalized)

• For qubit, \(\rho=\begin{pmatrix}|a|^2 & ab^*\\ a^*b & |b|^2\end{pmatrix}\)

• Properties

  1. \(\rho^+=\rho\)

  2. tr(\(\rho\)) = 1

  3. \(\rho\ge0\)

  4. 1 \(\rho^2=\rho\)(equivalent to 4. 2 tr\((\rho^2)=1\))

• Use unitary normalization to use {1,2,3,4.2} to prove the form of \(\rho=|\phi><\phi|\)

• For qubit

• \(|\psi>=a|0>+b|1>=cos\frac \theta 2|0>+e^{i\phi}sin\frac \theta 2|1>\) on the Bloch sphere

  
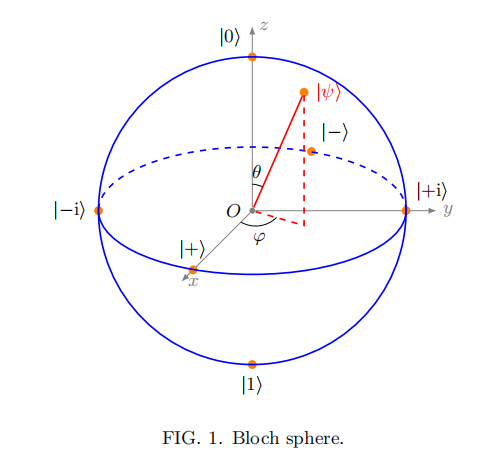
  • \(|+y>=|+i>,|-y>=|-i>\)

• The meaning of 3 coordinates

  Z: \(cos \theta=cos^2\frac \theta 2-sin^2\frac \theta 2=Pr(Z=1)-Pr(Z=-1)=<\sigma_z>\)

  X: \(<\sigma_x>\), Y: \(<\sigma_y>\)

• Orthogonal states in Bloch sphere

• \((x_1,y_1,z_1),(x_2,y_2,z_2)\) opposite orientation

• Bases

  \(\mathcal Z=\{|0>,|1>\}, \mathcal X = \{|+>,|->\},\mathcal Y=\{|+i>,|-i>\}\)

• Pauli matrix

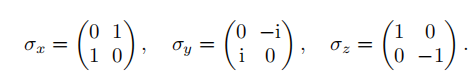
and \(\sigma_0=I\) (relation between Pauli matrix and the XYZ coordinates)

• Eigenvectors and eigenvalues

  \(\sigma_x-|+>,|->\), \(\sigma_y-|+i>,|-i>\), \(\sigma_z-|0>,|1>\)

• Mutually unbiased states(MUB: \(X,Y,Z\))

  \(|<0|+>|^2=\frac 12\)

• In MUB, for 2 bases \(\{|\psi_i>\}_{i\in[d]},\{|\phi_i>\}_{j\in[d]}\)

  \(\forall i,j, |<\psi_i|\phi_j>|^2=\frac 1d\).

  If d is prime or prime power, d+1 MUB (why only one MUB for d=3)

  For any d, the number of MUB is no more than d+1, no less than 3

• Observable and Measurement

• In Q.M., an observable is a self-adjoint operator

  1. Linear

  2. Adjoint

  \(<\psi|A\phi>=<A^+\psi|\phi>\)

  3. Projectors (for non-degenerate cases)

  \(E_i=|\psi_i><\psi_i|\), and \(E_iE_j=\delta_{ij}E_i\), we can write

  \(A=\sum_ia_i|i><i|\)

• When we measure an observable A, we'll get \(a_i\) with probability \(|<\psi|\phi_i>|^2=<\psi|E_i|\psi>=tr(E_i|\psi><\psi|)\), the average outcome is

  \(< a >=\sum_ia_iPr(a_i)=<\psi|A|\psi>\)

• After measurement, the state transfers to \(\frac{E_i|\psi>}{||E_i|\psi>||}\)